素数を見てみよう
注意: この記事では色を扱います。人およびコンピュータによっては筆者の想定した見え方とは異なって見える可能性があるのでご注意ください。
素数大富豪 Advent Calendar 2022 - Adventar 10日目の記事です。
昨日の記事は、999999チェックについて - まもめも でした。
6桁の足し算より3桁の加減算のほうが速いと感じるのは私だけでしょうか。
さて、本日の記事は「素数を見てみよう」ということで、早速見てみましょう。
画像

どんなパターンが見えるでしょうか。右下の暗い6マス、上端の薄黄色、全体的になんとなく見える右上がりの線など、いくつかの特徴的な要素が目に入りますね。
ところで、これのどこが素数なのでしょう。実は、この画像には3枚出し素数が全て含まれているのです。それでは、この画像がどうやって作られたか見てみましょう。
解説
マスの数を数えてみると、この画像が13×13マスからなることがわかります。各マスは、3枚出しのうち上2枚に対応しています。縦軸が1枚目で、横軸が2枚目です。左と上から順にA,2,3,...,T,J,Q,Kとなっているので、たとえば左上の暗い青のマスはAAX、右中央の緑の1マスは6TXに対応します。
マスの色は、3枚目に何を使うと素数になるかを示しています。素数として可能な一番下の位のカードは1,3,7,9,J,Kの6通りあるので、マスの色は2^6=64通り考えられます。あとはこの64通りをいかにしていい感じの色に割り当てるかが問題で、これは各個人の裁量に任せられます。
私は、このように配置しました。
色の選択
素数のヒートマップのようにしたかったので、素数の個数が多いほど白に近くなるようにしました。素数なしは黒、6枚全て素数は白です。改めて画像を見ると、真っ白なセルがないことがわかると思います。なぜそうなるかは、読者への演習問題とします。
同じ素数の個数での色の配置には、色相を使いました。大きいカードから比較したときに小さい順(昇順)に、色相環上で並ぶようにしました。
たとえば、
1枚の時は{1},{3},{7},{9},{J},{K}
2枚の時は{1,3},{1,7},{3,7},{1,9},{3,9},{7,9},{1,J},{3,J},{7,J},{9,J},{1,K},{3,K},{7,K},{9,K},{J,K}
のように並べました。
小さい方が赤で、大きい方が青~紫となるように配置したので、紫系の色が含まれているマスではJやKを3枚目に使うと素数になることを意味しています。
彩度の情報も使いたかったのですが、うまい方法が思いつきませんでした。
パターンを具体的な数値で見てみる
これを、素数を覚える手がかりにできたら理想ですね。いくつかのパターンで、実際にどのような素数があるか確認してみましょう。
右下の暗い色6マス
TQ -> {}
JQ -> {J}
QQ -> {}
JK -> {A}
QK -> {K}
KK -> {J}
あまり覚える手立てにはならなさそうですね。
上端の薄黄色
A9 -> {1,3,7,9,K}
A9のマスは非常に面白い性質を持っています。なぜなら、同じ上2枚で3枚出し素数が5個作れるのは{1,3,7,9,K}のパターンしかなく、しかもそれがA9でしか起こらないからです。
さらなる発展
さて、最近の素数大富豪では3枚出しを覚えている人も多くなり、3枚では無双できなくなってきました。それでは、4枚出しを見てみましょう。最初のカードごとに画像を生成します。
それでは、13枚一気にどーん!













数が大きくなるにつれ素数が減って色が暗くなっていくのがよくわかりますね。
みなさんはの好きなパターンはあったでしょうか。私は、KXXXの右下の巨大黒色領域に燦然と輝く青マスが好きです。
相互リンク
明日はpn_122051さん(OTTYさん)による「合成数大富豪楽しいね!的な記事書きたい」です。
合成数を素因数で色分けしてみるのも面白いかもしれません。
素因数分解の定石を整理する
素因数分解がガチプロスポーツになってしまったので、初心者の私は定石を明文化することにしました。
また、これらの定石で対応できる数の割合もプログラミングを使って調べました。
対照実験: 全ての数を素数とみなす
問題として出された数をそのまま返す方法です。実用性は全くありませんが、対照実験として割合を掲載します。
正しく判定できる割合
4桁: 1061/9000(11.8%)
5桁: 8363/90000(9.3%)
6桁: 68906/900000(7.7%)
定石1: 2,3,5の倍数を調べる
非数学徒にもよく知られた方法です。2と5の倍数は1の位、3の倍数は桁ごとの和で調べられます。
これだけで48以下の数は全て正しく判定できるだけでなく、4桁であれば判定の精度は50%を超えます。
正しく判定できる割合
4桁: 5067/9000(56.3%)
5桁: 38253/90000(42.5%)
6桁: 303230/900000(33.7%)
定石2: 7,11,13の倍数を調べる
素数大富豪プレイヤーにはよく知られた方法ですが、1001=7×11×13なので与えられた数を1001で割ることで7,11,13の倍数判定を同時に行うことができます。
289=17^2未満は正しく判定できます。
この時点で6桁の数でも50%以上を正しく判定できます。
正しく判定できる割合
4桁: 7314/9000(81.3%)
5桁: 57970/90000(64.4%)
6桁: 460038/900000(51.1%)
定石3: 23,29の倍数を調べる
17,19よりも計算が簡単なのでこちらを先に書きます。23×29×3=2001であることを利用します。
正しく判定できる割合
4桁: 7700/9000(85.6%)
5桁: 63245/90000(70.3%)
6桁: 509869/900000(56.7%)
定石4: 17,19の倍数を調べる
17×19×3=1000-31であることを利用します。少し面倒です。しかし、これでついに4桁の割合が90%を超えます。
正しく判定できる割合
4桁: 8405/9000(93.4%)
5桁: 71817/90000(79.8%)
6桁: 589097/900000(65.5%)
定石5: 平方数を足すと平方数
平方数を足して平方数になるかを調べます。もしなる場合は、2乗-2乗の形にできるので因数分解できます。
元の数自体が平方数である場合もここに含まれます。
正しく判定できる割合: 0^2から10^2まで調べた場合
4桁: 8605/9000(95.6%)
5桁: 74250/90000(82.5%)
6桁: 605776/900000(67.3%)
4桁の判定失敗が395個にまで減りました。
定石∞: ルックアップテーブル
せっかくなので、残りの395個を分類して全列挙してみましょう。
途中で諦めるパターン
3286=2×1643(実際には2×31×53)のように、395個の中には小さい4桁の素因数分解で失敗するケースが重複して数えられているものがあります。
このようなパターンは116個あり、取り除いた残りは279個です。
実は自明なパターン
ここまで来て見逃しているパターンがありました。それは、101の倍数です。
279個のうち101の倍数は12個あり、取り除いた残りは267個です。
2桁の掛け算
残りは全て2桁×2桁か2桁×3桁の強者ぞろいです。2桁は31から83まで多岐にわたり、覚えるしかありません。
以下にリストを示します。覚えられるもんなら覚えてみやがれください。
31×53=1643 31×59=1829 31×61=1891 31×67=2077 31×71=2201 31×73=2263 31×79=2449 31×83=2573 31×89=2759 31×97=3007 31×103=3193 31×107=3317 31×109=3379 31×113=3503 31×127=3937 31×131=4061 31×137=4247 31×139=4309 31×149=4619 31×151=4681 31×157=4867 31×163=5053 31×167=5177 31×173=5363 31×179=5549 31×181=5611 31×191=5921 31×193=5983 31×197=6107 31×199=6169 31×211=6541 31×223=6913 31×227=7037 31×229=7099 31×233=7223 31×239=7409 31×241=7471 31×251=7781 31×257=7967 31×263=8153 31×269=8339 31×271=8401 31×277=8587 31×281=8711 31×283=8773 31×293=9083 31×307=9517 31×311=9641 31×313=9703 31×317=9827
37×59=2183 37×61=2257 37×67=2479 37×71=2627 37×73=2701 37×79=2923 37×83=3071 37×89=3293 37×97=3589 37×103=3811 37×107=3959 37×109=4033 37×113=4181 37×127=4699 37×131=4847 37×137=5069 37×139=5143 37×149=5513 37×151=5587 37×157=5809 37×163=6031 37×167=6179 37×173=6401 37×179=6623 37×181=6697 37×191=7067 37×193=7141 37×197=7289 37×199=7363 37×211=7807 37×223=8251 37×227=8399 37×229=8473 37×233=8621 37×239=8843 37×241=8917 37×251=9287 37×257=9509 37×263=9731 37×269=9953
41×67=2747 41×71=2911 41×73=2993 41×79=3239 41×83=3403 41×89=3649 41×97=3977 41×103=4223 41×107=4387 41×109=4469 41×113=4633 41×127=5207 41×131=5371 41×137=5617 41×139=5699 41×149=6109 41×151=6191 41×157=6437 41×163=6683 41×167=6847 41×173=7093 41×179=7339 41×181=7421 41×191=7831 41×193=7913 41×197=8077 41×199=8159 41×211=8651 41×223=9143 41×227=9307 41×229=9389 41×233=9553 41×239=9799 41×241=9881
43×67=2881 43×71=3053 43×73=3139 43×79=3397 43×83=3569 43×89=3827 43×97=4171 43×103=4429 43×107=4601 43×109=4687 43×113=4859 43×127=5461 43×131=5633 43×137=5891 43×139=5977 43×149=6407 43×151=6493 43×157=6751 43×163=7009 43×167=7181 43×173=7439 43×179=7697 43×181=7783 43×191=8213 43×193=8299 43×197=8471 43×199=8557 43×211=9073 43×223=9589 43×227=9761 43×229=9847
47×71=3337 47×73=3431 47×79=3713 47×83=3901 47×89=4183 47×97=4559 47×103=4841 47×107=5029 47×109=5123 47×113=5311 47×127=5969 47×131=6157 47×137=6439 47×139=6533 47×149=7003 47×151=7097 47×157=7379 47×163=7661 47×167=7849 47×173=8131 47×179=8413 47×181=8507 47×191=8977 47×193=9071 47×197=9259 47×199=9353 47×211=9917
53×79=4187 53×83=4399 53×89=4717 53×97=5141 53×103=5459 53×107=5671 53×109=5777 53×113=5989 53×127=6731 53×131=6943 53×137=7261 53×139=7367 53×149=7897 53×151=8003 53×157=8321 53×163=8639 53×167=8851 53×173=9169 53×179=9487 53×181=9593
59×83=4897 59×89=5251 59×97=5723 59×103=6077 59×107=6313 59×109=6431 59×113=6667 59×127=7493 59×131=7729 59×137=8083 59×139=8201 59×149=8791 59×151=8909 59×157=9263 59×163=9617 59×167=9853
61×83=5063 61×89=5429 61×97=5917 61×103=6283 61×107=6527 61×109=6649 61×113=6893 61×127=7747 61×131=7991 61×137=8357 61×139=8479 61×149=9089 61×151=9211 61×157=9577 61×163=9943
67×89=5963 67×97=6499 67×103=6901 67×107=7169 67×109=7303 67×113=7571 67×127=8509 67×131=8777 67×137=9179 67×139=9313 67×149=9983
71×97=6887 71×103=7313 71×107=7597 71×109=7739 71×113=8023 71×127=9017 71×131=9301 71×137=9727 71×139=9869
73×97=7081 73×103=7519 73×107=7811 73×109=7957 73×113=8249 73×127=9271 73×131=9563
79×103=8137 79×107=8453 79×109=8611 79×113=8927
83×107=8881 83×109=9047 83×113=9379
もし応用情報の計算量が応用計算並みに多かったら
随時問題を追加します。解答は用意しておりませんが、応用情報ドットコムなどで同じ種類の過去問の解説を読めば計算方法は分かると思います。
(1) 処理に59.9nsかかる命令が24%、17.7nsかかる命令が76%からなる命令ミックスによるコンピュータの処理性能は、何MIPSですか。(MIPSの小数第1位未満四捨五入)
(2) 稼働率が60.8%, 76.4%, 74.2%のシステムを直列に並べたシステムがある。このシステムの稼働率はいくらですか。(パーセントの小数第1位未満四捨五入)
(3) あるCPUのキャッシュメモリのヒット率は82.1%、キャッシュメモリのアクセス時間は38.1ms、主記憶のアクセス時間は93.5msである。このCPUの実行アクセス時間は何ミリ秒ですか。(ミリ秒の小数第1位未満四捨五入)
(4) あるシステムのMTBFは137時間25分であり、MTTRは3時間58分である。このシステムの稼働率はいくらですか。(パーセントの小数第1位未満四捨五入)
(5) 21.798Mバイトのデータを565kビット/秒の回線を使って伝送するとき、転送時間は何秒ですか。ただし、回線の伝送効率を55%とし、1Mバイト=10^6バイト、1kビット=10^3ビットとする。(秒未満四捨五入)
(6) 回線速度が64,000ビット/秒の回線を使ってデータを連続送信したとき、平均して131.8秒に1回の1ビット誤りが発生した。この回線のビット誤り率はいくらですか。(10%を1分とし、埃未満四捨五入)
(7) 売上高が\4,051,381のとき\1,045,742の損失、売上高が\6,881,098のとき\292,116の利益と予想された。損益分岐点は何円ですか。(円未満四捨五入)
筋肉に固定資産税をかける方法
今更ですが、何年か前に筋肉の多い人に対して
「デカすぎて固定資産税がかかりそうだな!」
と声を掛けるのが流行りました。
そこで、この記事ではどのようにすれば筋肉に固定資産税をかけることができるか検証します。
注意: 私は弁護士ではないので、法律の解釈を誤っている可能性があります。その場合はコメントでご指摘ください。
以下、地方税法の条文は全てe-Gov法令検索から引用しています。
固定資産税って何?
そもそも、固定資産税は何にかかるのでしょうか。地方税法第343条第1項には、
「固定資産税は、固定資産の所有者(質権又は百年より永い存続期間の定めのある地上権の目的である土地については、その質権者又は地上権者とする。以下固定資産税について同様とする。)に課する。」
と書かれています。つまり、筋肉を固定資産にすることができれば筋肉に固定資産税をかけることができるようですね。
固定資産って何?
では、固定資産とは何なのでしょう。地方税法第341条1項には、
「固定資産 土地、家屋及び償却資産を総称する。」
と書かれています。この条文は定義の一部なので、「固定資産とは、土地と家屋と償却資産の総称である。」という意味だととれます。筋肉は明らかに土地でも家屋でもないので、筋肉を何らかの方法で償却資産にすることができれば、筋肉に固定資産税をかけることができます。
償却資産って何?
用語がどんどんたらい回しにされるだけで、まだ具体的な方法が出てきません。根気良く、次の定義を見ていきましょう。同じ地方税法第343条の第4項には、
「償却資産 土地及び家屋以外の事業の用に供することができる資産(鉱業権、漁業権、特許権その他の無形減価償却資産を除く。)でその減価償却額又は減価償却費が法人税法又は所得税法の規定による所得の計算上損金又は必要な経費に算入されるもののうちその取得価額が少額である資産その他の政令で定める資産以外のもの(これに類する資産で法人税又は所得税を課されない者が所有するものを含む。)をいう。ただし、自動車税の種別割の課税客体である自動車並びに軽自動車税の種別割の課税客体である原動機付自転車、軽自動車、小型特殊自動車及び二輪の小型自動車を除くものとする。」
と書いてあります。長いですが、定義文は「XでYのうちZ以外のものをいう。ただし、Wを除くものとする。」という構造になっています。つまり、集合の表記で書けば(X∩Y-Z)-Wです。
つまり、筋肉が償却資産になるためには、筋肉がXでもYでもあり、ZでもWでもなければよいですね。
では、XYZWをそれぞれ見ていきましょう。
X: 土地及び家屋以外の事業の用に供することができる資産(鉱業権、漁業権、特許権その他の無形減価償却資産を除く。)
さっそく問題が生じました。個人所有の筋肉はXの「事業の用に供することができる資産」の条件に反してしまいます。その個人を個人事業主に仕立て上げて、続けましょう。
Y: その減価償却額又は減価償却費が法人税法又は所得税法の規定による所得の計算上損金又は必要な経費に算入されるもの
もっと大きな問題です。筋肉を購入して減価償却しないと固定資産税の対象にはなりません。おそらく自身の筋肉はこの条件を満たしようがないので、何らかの動物の筋肉を合法的な手段で手に入れたものとしましょう。この時点で本来の趣旨からはだいぶ外れていますが、筋肉に固定資産税をかけるにはこうするしかありません。
Z: その取得価額が少額である資産その他の政令で定める資産以外のもの(これに類する資産で法人税又は所得税を課されない者が所有するものを含む。)
10万円以下だと少額とみなされ、20万円以下だと課税対象とならないらしいので、20万円を超える必要があります。また、償却資産の合計が150万円以下だと課税されないので、何か適当に固定資産を買っておきましょう。
W: 自動車税の種別割の課税客体である自動車並びに軽自動車税の種別割の課税客体である原動機付自転車、軽自動車、小型特殊自動車及び二輪の小型自動車
筋肉は自動車ではないので、この条件は自動的に満たされます。
減価償却
筋肉を減価償却するにはどうすればよいでしょうか。
国税庁のサイトによると、減価償却は時間で価値が減少するものに付けられます。筋肉は生ものなので当然時間で価値が減少します。すなわち、減価償却できる可能性があります。おそらく耐用年数は備品扱いで8年になるものと思われますが、本当にそれでいいのかは分かりません。
結論
筋肉に固定資産税をかけるには、自分以外の何らかの動物の筋肉を150万円分以上購入し、それを8年(たぶん)で減価償却すればよいことがわかりました。
これだけの金額ともなると、筋肉質の動物を直接購入してしまうのもありかもしれませんね。
正十六胞体って何?別名がある?双対は?4次元図形の謎に迫る!
昨日の記事は
でした。
複素平面との関係を感じたのですが、今後の記事で触れられるのでしょうか。
今日は12月16日です。
16と言えば、正十六胞体ですね。
正十六胞体って、どんな図形なのでしょう?
正十六胞体の基本的性質について調べてみました。
正十六胞体って何?
正十六胞体は、
4次元の正軸体で、
16個の正四面体から構成されています。
正軸体というと
3次元では
正八面体がそうですね。
つまり、
正十六胞体は
正八面体の4次元バージョン
といえそうです。
正八面体は四角錐を
底面で2つ貼り合わせた
ものなので、
正十六胞体は正八面体錐を
底胞で2つ貼り合わせた
ものとも言えますね。
正十六胞体の別名は?
正十六胞体は英語で
Hexadecachoron(ヘキサデカコロン)
というそうです。
数学者のJonathan Bowersは
この立体に
Hex(ヘックス)
という略称を付けました。
おそらく
Hexadecachoronの
最初の3文字です。
正十六胞体の双対は?
4次元立体の双対は
胞が点に
面が辺に
辺が面に
点が胞に
なります。
それでは
正十六胞体の双対は
一体何なのでしょうか。
なんと
正十六胞体の双対は
超立方体です!
3次元でも
正八面体の双対は
立方体なので
似たような感じなのかも
しれませんね。
正十六胞体はどう見える?
ここまできたら
正十六胞体を
見てみたくなりますね。
4次元の図形なので
直接見ることはできませんが
3次元に描いた絵なら
見ることができます。
まず3次元の
正八面体の絵が
どんな形をしているか
復習してみましょう。
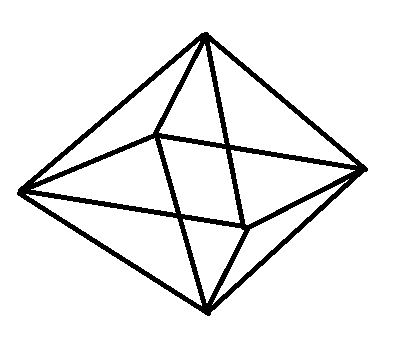
この絵を2次元の図形だと思ってみると、
真ん中の潰れた正方形の各頂点から
上下の頂点に向かって線が伸びている
絵だということが分かります。
ということは
正十六胞体の絵は
こんな感じになるのでしょうか。

Wikipediaも見てみたのですが、
二次元の幾何学模様にしか見えませんね。
正十六胞体には仲間がいる?
どうやら英語版Wikipediaによると
rectifiedとか
cantellatedとか
runcinatedとか
いろいろあって
図を見ているだけでも
4次元の神秘に
触れられそうです。
まとめ
正十六胞体という
4次元図形について
調べてみましたが
よくわかりませんでした。
いかがでしたか?
明日の記事は
です。
当記事を書くにあたって、以下の記事を参考にした。
[1] りょりょ. 「綾瀬はるかの現在の彼氏が確定!彼氏はどんな人?馴れ初めは?結婚の予定は?」. 芸能ゴシップ. https://芸能ゴシップネタ.com/2020/07/02/haruka-ayases-current-boyfriend-is-confirmed-what-kind-of-person-is-your-boyfriend-how-did-you-get-used-to-it/. (参照日2020年11月29日).
[2] 年収図鑑. 「小坂菜緒の年収がヤバい!不遇のけやき坂時代を乗り越えて…!」. https://italyseek.net/2020/10/09/%e5%b0%8f%e5%9d%82%e8%8f%9c%e7%b7%92%e3%81%ae%e5%b9%b4%e5%8f%8e%e3%81%8c%e3%83%a4%e3%83%90%e3%81%84%ef%bc%81%e4%b8%8d%e9%81%87%e3%81%ae%e3%81%91%e3%82%84%e3%81%8d%e5%9d%82%e6%99%82%e4%bb%a3%e3%82%92/. (参照日2020年11月29日).
[3] ロバ耳日誌運営事務局. 「宮崎謙介の離婚理由と元妻加藤鮎子の現在は|金子恵美とは離婚しない根拠は?」. ロバ耳日誌. https://robamimireport.com/miyazaki-kensuke-rikon-riyuu/. (参照日2020年11月29日).
13平均律~魔界の音楽~
「魔入りました! 入間くん」では、魔界(悪魔の世界)を主題としている。魔界では、13や666といった数字がよく使われる。
そこで私は思った。
魔界の音楽も1オクターブが13音なのだろうか。だとしたら、どんな音楽理論が展開されているのだろうか。
そこで、このブログでは13平均律を考えることにする。
第1章 音名
その前に、まず12平均律について復習する。音名とセント数は、以下の通りである。いつものである。

13平均律では、セント数は次のようになる。C以外はまだわからないので空欄とした。

空欄のうち両端は簡単に埋めることができる。しかし、真ん中は難しい。完全4度と完全5度が存在しないのだ。

ここでは、次のように埋めることにする。また、3段目に度数を示した。4度と5度が完全ではなくなることに注意せよ。

11倍音がほぼぴったりだが、3倍音、5倍音、7倍音はことごとく外れている。
第2章 和音
音名が決まったので和音を考えたいわけだが、3度と5度のそれぞれに長短があるためもっとも単純な3和音ですら4種類存在する。

ここで重要なことは、長3度ですら純正の長3度(5:6, 386セント)より短いということである。
実際に聞いてみよう。Cm, CmM5, CMm5, Cの順で流れる。
全体的に暗い感じがする。それもそのはず、長3度ですら純正の長3度(386セント)に達していないからである。もしかしたら悪魔にはこれでちょうどいいかもしれない。
最終章 音源
音律ができたからには、ドレミの歌を歌ってみたくなる。そこで、いつものように重音テトに歌ってもらうことにした。明らかにファの位置がおかしいが、そこしかないので仕方ない。
重音テト「これ音程合ってますか?」
因数分解
この記事は、先日行われたロマンティック数学ナイトにインスパイアされたものです。
(注意)この記事は、全編小学校の算数のような文体で進行します。
太郎くんと花子さんは、次のようなゲームをしています。
・花子さんは、\( 0 \)でない整数を3つ決めて、太郎くんに伝えます。
・太郎くんは、3つの整数を並べ替えて、それらの係数に持つような\( x \)の2次式を作ります。
・太郎くんがその2次式を因数分解できたら太郎くんの勝ち、できなかったら花子さんの勝ちです。
花子「じゃあ、次は\( 1, 2, 3\)でやってみて。」
太郎「そうだな、\( x^2 + 3x + 2 = (x+1)(x+2) \)だから、僕の勝ちだね。」
花子「\( 1, 1, 3 \)だったらどうかな。」
太郎「\( x^2 + 3x + 1 = \cdots \)ぐぬぬ。因数分解できないぞ。君の勝ちだ。」
それを見ていた京子さんと大地くんが話しています。
京子「このゲームは、花子さんが適切な数を選べば毎回勝てるんじゃないかな。」
大地「そうだね。少し考えてみよう。」
京子「まず、一般の2次式\( Ax^2 + Bx + C \)が因数分解できるときはどんな時か考えてみよう。」
大地「因数分解と言っても、どの範囲で因数分解するか決めないといけないね。」
京子「太郎くんは整数の範囲でしか因数分解していないみたいだから、整数の範囲で考えてみよう。」
大地「\( Ax^2 + Bx + C \)の判別式は\( B^2 - 4AC \)だから、\( B^2 - 4AC \)が平方数になることは\( Ax^2 + Bx + C \)が整数の範囲で因数分解できることの必要条件だね。」
京子「そうだね。だから、\( A, B, C \)をどう並べ替えても\( B^2 - 4AC \)が平方数にならないようにすればいいね。」
大地「もし\( A \)や\( C \)が大きかったら、\( B^2 - 4AC \)は負になるから絶対に平方数にはならないね。」
京子「でも、その大きい数が\( B \)のところに入ったらどうしよう。」
大地「\( B \)がすごく大きかったら、\( B^2 - 4AC \)は\( (B-1)^2 \)と\( B^2 \)の間に入って、平方数にならないんじゃないかな。」
京子「そうだね。」
京子さんは、次のような証明を行いました。
\( 0 < 4A^2 < 4C^2 < B \)とする。
このとき、
\( \begin{align*} & B^2 - 4AC \\ &= B^2 - \sqrt{4A^2 \cdot 4C^2} \\ &> B^2 - \sqrt{B \cdot B} \\ &= B^2 - B \\ &= B^2 - 2B + 1 + (B-1) \\ &> (B-1)^2 \end{align*} \)
であるから、\( (B-1)^2 < B^2-4AC < B^2 \)が成り立つ。
1週間後、太郎くんと花子さんはまた同じゲームをしていました。
花子「京子さんに必勝法を聞いたんだよね。\( 1, 2, 17\)」
太郎「実は昨日解の公式を覚えてきたんだ。\( x^2 + 17x + 2 = \left( x - \frac{-17+\sqrt{281}}{2} \right)\left( x - \frac{-17-\sqrt{281}}{2} \right) \)だね。I WIN!」
花子「(; ・`д・´) ナ、ナンダッテー !! (`・д´・ (`・д´・ ;)」
京子さんたちもその様子を見ていました。
京子「今度は太郎くんが実数の範囲で因数分解を始めたね。」
大地「この場合は、整数のときと同じようにはいかないね。」
京子「でも、\( Ax^2 + Bx + C \)が実数の範囲で因数分解できる必要十分条件は、\( B^2 - 4AC \)が\( 0 \)以上であることだから、判別式が使えそうだよ。」
大地「つまり、花子さんは\( a^2 - 4bc < 0, b^2 - 4ca < 0, c^2 - 4ab < 0 \)を満たす\( 0 \)でない整数\( a, b, c \)を選べばいいね。」
京子「でも、そんな整数ってあるのかな。」
大地「たとえば、\( a = b = c = 1 \)があるね。」
京子「この条件を満たす整数の組は、全部でいくつあるんだろう。」
大地「ある\( (a, b, c) \)が条件を満たすなら、\( a \)と\( b \)と\( c \)に\( 0 \)以外の数を掛けても条件を満たすから、無限にあるね。」
京子「ということは、条件を満たす点からなる\( abc \)空間上の点を考えると、原点を通る同じ直線上にある格子点は、原点以外は全部条件を満たすか、全部条件を満たさないかのどちらかだね。」
大地「ということは、単位球面上の点を考えるとうまく図示できそうだね。」
京子「単位球面上の点のうち、条件を満たす\( (a,b,c) \)の組を色で塗って、縦軸を緯度、横軸を経度とする地図に描いてみたよ。緯度経度は赤道が\( c = 0 \)、北極が\( (0, 0, 1) \)、本初子午線が\( (1,0,0) \)を通るように取ったよ。ここでは\( (a,b,c) \)は実数としたことに注意してね。」

大地「東半球では、南半球には条件を満たす点はないんだね。」
京子「東半球では\( b > 0 \)で、南半球では\( c < 0 \)だから、\( a^2 - 4bc \)が必ず正になってしまうからだよ。」
太郎「ねぇねぇ、そのWi-Fiみたいな図形は何?」
京子「君たちのやっているゲームを図にしてみたよ。花子さんが最初に選んだ数がWi-Fiの圏内に入れば、花子さんが絶対に勝つよ。」
太郎「難しそうなことをやっているんだね。」
先生「おーい、授業始まるぞー、今日は一様多面体についてだからな、よく聞いとけよ!」